А. Антропов
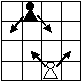
Задача №1. Какое наибольшее количество белых и чёрных пешек можно расставить на клетчатой доске $9 \times 9$ (пешку, независимо от её цвета, можно ставить на любую клетку доски) так, чтобы никакая не била никакую (в том числе и своего цвета)? Белая пешка бьет две соседние по диагонали клетки на соседней горизонтали с бoльшим номером, а чёрная — две соседние по диагонали клетки на соседней горизонтали с меньшим номером (см. рисунок).
комментарий/решение(1) олимпиада
Задача №2. В треугольнике $ABC$ сторона $AB$ больше стороны $BC$. На продолжении стороны $BC$ за точку $C$ отметили точку $N$ так, что $2BN = AB+BC$. Пусть $BS$ — биссектриса треугольника $ABC$, $M$ — середина стороны $AC$, а $L$ — такая точка на отрезке $BS$, что $ML \parallel AB$. Докажите, что $2LN = AC$. ( А. Антропов )
комментарий/решение(2) олимпиада
Задача №3. а стороне $AB$ треугольника $ABC$ выбрана точка $P$, а на сторонах $AC$ и $BC$ точки $S$ и $T$ таким образом, что $AP=AS$ и $BP=BT$. Описанная окружность треугольника $PST$ вторично пересекает стороны $AB$ и $BC$ в точках $Q$ и $R$ соответственно. Прямые $PS$ и $QR$ пересекаются в точке $L$. Докажите, что прямая $CL$ делит отрезок $PQ$ пополам. ( А. Антропов )
комментарий/решение(1) олимпиада