Temirlan Satylkhanov

Задача №1. (Тима и Рама) На доске в ряд написано $N$ целых чисел. Темірлан и Рамазан играют в следующую игру:

Они будут ходить по очереди, первым начинает Темірлан.
На каждом ходу игрок может стереть с доски любое ненулевое количество чисел с начала, или с конца. Но нельзя стереть все числа.
Игра закончится, когда на доске останется ровно одно число. Темірлан хочет минимизировать последнее число, а Рамазан хочет максимизировать это число.

Пока Темірлан отошел, Рамазан хочет стереть ровна $K$ чисел. Он может стереть любые числа. Когда Темірлан вернется, они начнут играть как обычно, но на доске будет написано $N-K$ чисел.
Для каждого из $Q$ чисел $K_1,K_2, ..., K_Q$, Рамазан хочет узнать, какое значение у последнего оставшегося числа, если он заранее сотрет $K_i$ чисел, и оба игрока играют оптимально?

Формат входных данных:

В первой строке находится одно целое число $N$.
Во второй строке находятся $N$ целых числа $A_1,A_2,...,A_N (1 \le A_i \le 10^6)$ --- числа написанные на доске.
В третьей строке находится одно целое число $Q$.
В четвертой строке находятся $Q$ целых числа $K_1,K_2,...,K_Q(0 \le K_i \le N - 1)$.

Формат выходных данных:

Выведите через пробел $Q$ чисел, $i$-е из них, значения последнего оставшегося числа, если Рамазан заранее сотрет $K_i$ чисел.

Примеры:

1.Вход:

Ответ:

1 3 3 4

2.Вход:

Ответ:

5 5 5

3.Вход:

6
2 7 5 4 8 10
3
3 5 2

Ответ:

7 10 7

Замечание:

В первом тесте при $K=3$, Рамазану выгодно стереть первое,второе и четвертое числа.

Система оценки:

Задача содержит 50 тестов, каждая из которых весят 2 балла.
Ограничения которые присутствуют в тестах:

3 теста: Первые три теста является тестами из примеров
5 тестов: $1 \le N \le 3, Q = 1, K_1 = 0$
10 тестов: $1 \le N \le 100, Q = 1, K_1 = 0$
12 тестов: $1 \le N \le 10^5, 1\le Q \le 2, 0 \le K_i \le 1$
10 тестов: $1 \le N \le 10^5, 1 \le Q \le 10^5,0 \le K_i \le N - 1$
10 тестов: $1 \le N \le 10^6, 1 \le Q \le 10^6, 0 \le K_i \le N - 1$

( Temirlan Satylkhanov )
комментарий/решение(14) олимпиада

Задача №2. (Тима и Рама) На доске в ряд написано $N$ целых чисел. Темірлан и Рамазан играют в следующую игру:

Они будут ходить по очереди, первым начинает Темірлан.
На каждом ходу игрок может стереть с доски любое ненулевое количество чисел с начала, или с конца. Но нельзя стереть все числа.
Игра закончится, когда на доске останется ровно одно число. Темірлан хочет минимизировать последнее число, а Рамазан хочет максимизировать это число.

Формат входных данных:

Формат выходных данных:

Примеры:

1.Вход:

Ответ:

1 3 3 4

2.Вход:

Ответ:

5 5 5

3.Вход:

6
2 7 5 4 8 10
3
3 5 2

Ответ:

7 10 7

Замечание:

В первом тесте при $K=3$, Рамазану выгодно стереть первое,второе и четвертое числа.

Система оценки:

Задача содержит 50 тестов, каждая из которых весят 2 балла.
Ограничения которые присутствуют в тестах:

3 теста: Первые три теста является тестами из примеров
5 тестов: $1 \le N \le 3, Q = 1, K_1 = 0$
10 тестов: $1 \le N \le 100, Q = 1, K_1 = 0$
12 тестов: $1 \le N \le 10^5, 1\le Q \le 2, 0 \le K_i \le 1$
10 тестов: $1 \le N \le 10^5, 1 \le Q \le 10^5,0 \le K_i \le N - 1$
10 тестов: $1 \le N \le 10^6, 1 \le Q \le 10^6, 0 \le K_i \le N - 1$

( Temirlan Satylkhanov )
комментарий/решение(14) олимпиада

Задача №3.

Задача E. Na2a и уравнение

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Na2a много баловался на уроке информатики, и учитель в наказание ему придумал следующую задачу. Найти неотрицательное целое число $x$, такое что ($a_1 \oplus x) + (a_2 \oplus x) + ... + (a_n \oplus x) = S$, где $a_1,...,a_n,S$ — заданные числа. Здесь $\oplus$ обозначает операцию побитового XOR или исключающего ИЛИ. Данная операция существует во всех современных языках программирования, например, в языках C++ и Java она обозначена как <<$\string^$>>, в Pascal — как <>. Помогите Na2a решить данное уравнение.

Формат входного файла

В первой строке находятся два целых числа $n$, $S (1 \le n \le 10^5, 0 \le S \le 10^{12})$. Во второй строке находятся $n$ целых числа $a_1$, $a_2$, ..., $a_n(0 \le a_i \le 10^{12})$.

Формат выходного файла

Выведите -$1$, если уравнение не имеет неотрицательных решений. Иначе выведите такое $x(x \ge 0)$, что описанное в условии равенство выполняется. Если существует несколько ответов, выведите любой из них.

Система оценки

Данная задача содержит пять подзадач, в каждой подзадаче выполняются ограничения из условии и:

$n \le 1000, a_i,s \le 1000$. Оценивается в $7$ баллов.
$n = 2, a_i,s \le 10^{12}$. Оценивается в $22$ баллов.
$n \le 10^4, a_i,s \le 10^6$. Оценивается в $20$ баллов.
$n \le 10^5, a_i,s \le 5 \cdot 10^7$. Оценивается в $16$ баллов.
$n \le 10^5, a_i,s \le 10^{12}$. Оценивается в $35$ баллов.

Пример:

Вход

3 4
1 2 3

Ответ

\Note Таблица для исключающего ИЛИ.\\ 1 $xor$ 1 = 1, 1 $xor$ 0 = 1\\ 0 $xor$ 1 = 1, 0 $xor$ 0 = 0\\ Например, если $X$ = $109_{10}$ = $1101101_{2}$, $Y$ = $41_{10}$ = $101001_{2}$ тогда: $X$ $\oplus$ $Y$ = $68_{10}$ = $1000100_{2}$. ( Temirlan Satylkhanov )
комментарий/решение(2) олимпиада

Задача №4.

Задача F. Тренерский выбор Тимы

Ограничение по времени:

4 секунды

Ограничение по памяти:

256 мегабайт

Тима с недавних пор начал тренировать баскетбольные команды. Капитаном команды всегда выбирается игрок с максимальным ростом. Также он придумал свою формулу несовместимости игроков в одной команде. Формула зависит от роста всех игроков в команде. Несовместимость игроков в одной команде равняется сумме разниц роста между всеми игроками и ростом капитана. Более формально, пусть $h_1, h_2, ... , h_m$ это рост игроков команды, $mx = max(h_1, h_2, ..., h_m)$, тогда несовместимость = $\sum_{i=1}^{m} mx$-$h_i$. У Тимы есть $n$ игроков выстроенных в ряд, $i$-й из них имеет рост $a_i$. Он хочет разбить всех на $k$ команд, каждый игрок должен быть в ровно одной команде и команда должна состоять из игроков, которые составляют непрерывный отрезок в ряду. Тима хочет собрать команды так, чтобы суммарная несовместимость была минимальной. Помогите Тиме разбить на команды оптимально.

Формат входного файла

Первая строка входных данных содержит два целых чисел $n$ и $k$ ($1 \le n \le 10^5$, $1 \le k \le min(n, 20)$) — количество игроков в ряду и количество команд. Вторая строка содержит $n$ целых чисел $a_i$ ($1 \le a_i \le 10^6$) — рост $i$-го игрока слева в ряду в сантиметрах.

Формат выходного файла

Выведите единственное целое число — ответ на задачу.

Система оценки

Данная задача содержит шесть подзадач, в каждой подзадаче выполняются ограничения из условий:

$n \le 100$, $k = 1$. Оценивается в $5$ баллов.
$n \le 2000$. Оценивается в $11$ баллов.
$k = 2$. Оценивается в $8$ баллов.
$k = 3$. Оценивается в $15$ баллов.
$a_i \le a_{i+1}$, для всех $1 \le i < n$. Оценивается в $19$ баллов.
Ограничения из условия задачи. Оценивается в $42$ баллов.

Пример:

Вход

7 3
6 4 1 5 3 2 2

Ответ

Вход

5 2
4 1 5 5 6

Ответ

Вход

9 2
3 7 4 1 3 2 4 6 7

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №5.

Задача B. Яблоки

Ограничение по времени:

1 секунда

Ограничение по памяти:

64 мегабайта

Тима и его $N - 1$ друзей собирали яблоки. Для удобства пронумеруем всех числами от $1$ до $N$. У Тимы номер $1$. Тима заметил, что у него яблок больше чем у его друзей, и решил поделиться своими яблоками. Он дал всем остальным столько яблок, сколько у них было. Т.е если у кого-то было $X$ яблок, то Тима дал ему еще $X$ яблок. Затем человек с номером $2$ дал всем столько, сколько у них имелось на тот момент. И так далее до $N$-го человека. И в результате у всех оказалось одинаковое количество яблок. Тима хочет знать сколько яблок было у каждого в начале. Он помнит, что в начале у него было $A_1$ яблок.

Формат входного файла

В первой строке входных данных записано одно целое число $T(1\le T \le 1000)$ - количество тестов. В следующих $T$ строках находится по два целых числа $N$ ($1 \le N \le 50$),$1\le A_1\le 10^{16}$.

Формат выходного файла

Выведите $T$ — строк, в каждой строке выведите $-1$ если такое случае невозможно. Иначе выведите $N$ чисел $A_1,A_2, .., A_N$. Если существует несколько возможных ответов, выведите любой из них.

Система оценки

Данная задача содержит четыре подзадачи:

$1 \le T \le 50, N = 2, 1 \le A_1 \le 10^6$. Оценивается в $10$ баллов.
$1 \le T \le 50, N = 3, 1 \le A_1 \le 10^9 $. Оценивается в $15$ баллов.
$T = 1, 1 \le N \le 50, 1 \le A_1 \le 10^5$. Оценивается в $30$ баллов.
$1 \le T \le 1000, 1 \le N \le 50, 1 \le A_1 \le 10^{16}$. Оценивается в $45$ баллов

Пример:

Вход

2
3 13
2 10

Ответ

13 7 4 
10 6

Замечание

Первый тест: В начале 13, 7, 4. После 1-го : 2, 14, 8. После 2-го : 4, 4, 16. После 3-го: 8,8,8. ( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №6.

Задача E. Перевороты

Ограничение по времени:

1 секунда

Ограничение по памяти:

64 мегабайта

На столе подряд лежат $K$ листов бумаги. Дано число $N$. На каждом листе записаны все числа от 1 до $N$ ровно по одному разу, но некоторые из них записаны на видимой стороне, а остальные на обратной. Ваша задача - перевернуть некоторые листы так, чтобы максимизировать количество различных чисел на видимых сторонах.

Формат входного файла

На первой строке даны $N$ и $K$, так чтобы $N \times K\le 10^6$ при этом $ N \ge 1 $ и $K \ge 1$. На следующих $K$ строках идут описания листов. На $i+1$ строке, первое число это $m$ ($0 \le m \le N$) — количество чисел записанных на видимой стороне $i$-ого листа бумаги. Далее идут $m$ чисел которые написаны на видимой стороне $i$-го листа, каждый от $1$ до $N$.

Формат выходного файла

Выведите строку состоящий из $K$ символов. $i(1 \le i \le K)$ символ равняется 1 если надо перевернут, иначе 0. Если существует несколько ответов, вывести любой.

Система оценки

Данная задача содержит пять подзадач:

$1 \leq N \leq 10$, $1 \le K \le 10$. Оценивается в $11$ баллов.
$1 \leq N \le K$. Оценивается в $8$ баллов.
$1 \leq N \leq 100$. Оценивается в $15$ баллов.
$1 \leq N \times K \leq 5 \cdot 10^4$. Оценивается в $30$ баллов.
$1 \leq N \times K \leq 10^6 $. Оценивается в $36$ баллов.

Примеры:

Вход

Ответ

Вход

6 2
3 1 3 4
3 1 2 4

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №7.

Задача G. Секретные алгоритмы

Ограничение по времени:

2 секунды

Ограничение по памяти:

256 мегабайт

В стране Timart есть $N$ городов и $M$ двусторонних дорог. Города пронумерованы от $1$ до $N$. Известно, что с каждого города можно добраться до любого другого по существующим дорогам. Андрей спрятал свитки с секретными алгоритмами в городах Timart. В $i$-ом городе хранится $A_i$ свитков. Рамазан хочет украсть эти свитки. Он может украсть все свитки из города, в котором он находится. Рамазан может начать воровать с любого города. Чтобы не быть пойманным, он не будет использовать одну дорогу два раза подряд. Свитки каждого города можно украсть не более одного раза, посещать города можно по несколько раз. Помогите Рамазану украсть как можно больше свитков.

Формат входного файла

В первой строке входных данных содержится два целых числа $N$, $M$ ($1 \le N \le 5 \cdot 10^5$, $0 \le M \le 5 \cdot 10^5$). Во второй строке находятся $N$ целых чисел $A_1, A_2, \ldots, A_N$, где $A_i$ — количество свитков в $i$-ом городе. В следующих $M$ строках содержится по $2$ целых положительных числа, разделенных пробелом, $u_i$, $v_i$ ($1 \le u_i, v_i \le N, u_i \neq v_i$)— дорога соединяющая города $u_i$ и $v_i$. Известно, что между двумя городами не может быть больше одной дороги, и что никакая дорога не соединяет город с самим собой. Гарантируется, что между любыми двумя городами существует путь состоящий из заданных дорог

Формат выходного файла

Выведите одно целое число — максимальное количество свитков, которое может украсть Рамазан.

Система оценки

Данная задача содержит пять подзадач:

$1 \le N \le 100$,$M = \frac{N \cdot (N - 1)}{2}$, $1 \le A_i \le 300$, для всех $1 \le i \le N$. Оценивается в $7$ баллов.
$1 \le N \le 12$, $0 \le M \le 66$, $1 \le A_i \le 300$, для всех $1 \le i \le N$. Оценивается в $12$ баллов.
$1 \le N \le 10^5$, $M = N - 1$, $1 \le A_i \le 10^9$, для всех $1 \le i \le N$. Оценивается в $12$ баллов.
$3 \le N \le 10^5$, $M = N$, $1 \le A_i \le 10^9$, для всех $1 \le i \le N$. Оценивается в $25$ баллов.
$1 \le N \le 5 \cdot 10^5$, $0 \le M \le 5 \cdot 10^5$, $1 \le A_i \le 10^9$, для всех $1 \le i \le N$. Оценивается в $44$ балла.

Пример:

Вход

8 8
1 2 3 4 5 6 7 8
1 2
2 3
2 4
2 5
5 6
6 7
7 8
8 5

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №8.

Задача H. Тима и сумма степеней

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

У Тимы есть целое число $N$ и массив $A$ из $N$ целых чисел. Также у него есть два целых числа $M$ и $K$. Для каждого $i$ от $1$ до $N$-$M$+$1$ Тима хочет посчитать значение выражения $1^K \cdot A_{i} + 2^K \cdot A_{i + 1} + \cdots + M^K \cdot A_{i + M - 1}$. Помогите ему решить эту задачу.

Формат входного файла

В первой строке находятся три целых числа $N$($1 \le N \le 10^5$),$M$($1 \le M \le N$) и $K$($0 \le K \le 20$). Во второй строке находятся $N$ целых числа $A_1,A_2, \cdots, A_N$ ($1 \le A_i \le 10^9$).

Формат выходного файла

Выведите $N$-$M$+$1$ строк, в $i$-ой строке выведите остаток $1^K \cdot A_{i} + 2^K \cdot A_{i + 1} + \cdots + M^K \cdot A_{i + M - 1}$. при делении на $10^9 + 7$.

Система оценки

Данная задача содержит пять подзадач:

$1 \le N \le 100, 0 \le K \le 3,1 \le A_i \le 10$. Оценивается в $7$ баллов.
$1 \le N \le 10^4, 0 \le K \le 20,1 \le A_i \le 10^9$. Оценивается в $12$ баллов.
$1 \le N \le 10^5, 0 \le K \le 1,1 \le A_i \le 10^9$. Оценивается в $13$ баллов.
$1 \le N \le 10^5, K = 2,1 \le A_i \le 10^9$. Оценивается в $20$ баллов.
$1 \le N \le 10^5, 0 \le K \le 20,1 \le A_i \le 10^9$. Оценивается в $48$ баллов

Примеры:

Вход

5 3 2
1 2 3 4 5

Ответ

36
50
64

Вход

3 2 0
7 3 2

Ответ

10
5

Замечание

Пояснение к примеру 1: При $i = 1$, $1^K \cdot A_1 + 2^K \cdot A_2 + 3^K \cdot A_3$ = $1^2 \cdot 1 + 2^2 \cdot 2 + 3^2 \cdot 3 = 1 + 8 + 27 = 36$. При $i = 2$, $1^K \cdot A_2 + 2^K \cdot A_3 + 3^K \cdot A_4$ = $1^2 \cdot 2 + 2^2 \cdot 3 + 3^2 \cdot 4 = 50$. При $i = 3$, $1^K \cdot A_3 + 2^K \cdot A_4 + 3^K \cdot A_5$ = $1^2 \cdot 3 + 2^2 \cdot 4 + 3^2 \cdot 5 = 64$. ( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №9.

Задача F. Сделайте неотрицательным!

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Тима считает массив целых чисел хорошим если все числа в массиве неотрицательные. У Тимы есть массив $a$ состоящий из $n$ целых чисел. Тима хочет сделать его хорошим, для этого он может делать следующую операцию:

выбрать три целых числа $i,j, x$ такие, что $1 <= i,j <= n, i \ne j, 1 <= x <= 10^9$ и $a_i \ge x$, а затем из числа $a_i$ отнять $x$, а к числу $a_j$ прибавить $x$. Стоимость такой операции $|i - j| \cdot x$ тенге.

Помогите Тиме, потратив минимальное количество тенге сделать массив хорошим.

Формат входного файла

В первой строке находятся два целых числа $n, type (1 <= n <= 3 \cdot 10^5, 0 <= type <= 1)$. Во второй строке находятся $n$ целых числа $a_1,a_2, ..., a_n(-10^8 <= a_i <= 10^8)$. Гарантируется, что можно сделать массив $a$ хорошим.

Формат выходного файла

В первой строке выведите минимальное количество тенге, которое необходимо чтобы сделать массив хорошим. Если $type = 1$, во второй строке выведите одно целое число $k (0 <= k <= 2 \cdot n)$ — количество операции. В следующих $k$ строках выведите по три целых числа $i,j,x(1 <= i,j <= n, i \ne j, 1 <= x <= 10^9)$ — описания операций. Вам не надо минимизировать количество операций, но нужно минимизировать количество потраченных тенге. Если $type = 0$, то кроме минимального количество тенге, ничего выводить не надо.

Система оценки

Задача состоит из восьми подзадач:

Примеры из условия. Оценивается в 0 баллов.
$n <= 10, type = 0, -1 <= a_i <= 1$. Оценивается в 8 баллов.
$n <= 200, type = 0, -10 <= a_i <= 10, |a_1| + |a_2| + ... + |a_n| <= 400$. Оценивается в 16 баллов.
$n <= 10^5, type = 0, -10^8 <= a_i <= 10^8, a_1 + a_2 + ... + a_n = 0$. Оценивается в 12 баллов.
$n <= 2000, type = 0, -1 <= a_i <= 1$. Оценивается в 15 баллов.
$n <= 3 \cdot 10^5, type = 0, -10^8 <= a_i <= 10^8, a_1 + a_2 + ... + a_n = 1$. Оценивается в 13 баллов.
$n <= 3 \cdot 10^5, type = 0, -10^8 <= a_i <= 10^8$. Оценивается в 15 баллов.
$n <= 3 \cdot 10^5, type = 1, -10^8 <= a_i <= 10^8$. Оценивается в 21 баллов.

Примеры:

Вход

7 0
1 1 -1 0 -1 1 1

Ответ

Вход

4 1
4 -2 -2 1

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №10.

Задача F. Сделайте неотрицательным!

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

выбрать три целых числа $i,j, x$ такие, что $1 <= i,j <= n, i \ne j, 1 <= x <= 10^9$ и $a_i \ge x$, а затем из числа $a_i$ отнять $x$, а к числу $a_j$ прибавить $x$. Стоимость такой операции $|i - j| \cdot x$ тенге.

Помогите Тиме, потратив минимальное количество тенге сделать массив хорошим.

Формат входного файла

Формат выходного файла

Система оценки

Задача состоит из восьми подзадач:

Примеры из условия. Оценивается в 0 баллов.
$n <= 10, type = 0, -1 <= a_i <= 1$. Оценивается в 8 баллов.
$n <= 200, type = 0, -10 <= a_i <= 10, |a_1| + |a_2| + ... + |a_n| <= 400$. Оценивается в 16 баллов.
$n <= 10^5, type = 0, -10^8 <= a_i <= 10^8, a_1 + a_2 + ... + a_n = 0$. Оценивается в 12 баллов.
$n <= 2000, type = 0, -1 <= a_i <= 1$. Оценивается в 15 баллов.
$n <= 3 \cdot 10^5, type = 0, -10^8 <= a_i <= 10^8, a_1 + a_2 + ... + a_n = 1$. Оценивается в 13 баллов.
$n <= 3 \cdot 10^5, type = 0, -10^8 <= a_i <= 10^8$. Оценивается в 15 баллов.
$n <= 3 \cdot 10^5, type = 1, -10^8 <= a_i <= 10^8$. Оценивается в 21 баллов.

Примеры:

Вход

7 0
1 1 -1 0 -1 1 1

Ответ

Вход

4 1
4 -2 -2 1

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №11.

Задача G. Камень… Ножницы… Бумага...

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

$N + 1$ роботов будут участвовать в турнире по камень-ножницы-бумага и один из роботов ваш. В этом турнире каждый робот использует программу, представляющую собой серию ходов, каждый из которых должен быть одним из следующих: 'R'(камень), 'P'(бумага) или 'S'(ножницы). Бумага побеждает камень, камень побеждает ножницы, ножницы побеждает бумагу. Когда играет два робота, побеждает тот, кто первым сделал выигрышный ход. В начале каждый робот делает первый ход своей программы. Если ходы у них различны, один из них побеждает по правилам игры. Если ходы одинаковые, каждый робот выполняет следующий ход своей программы и т.д. Когда робот сделал последний ход своей программы и ему необходимо сделать следующий ход, то он делает первый ход своей программы. Если игра идет бесконечно долго, объявляется ничья. Вы случайном образом узнали программы своих $N$ соперников. Сделайте программу для своего робота, чтобы ваш робот мог победить любого другого робота.

Формат входного файла

В первой строке находится одно целое число $N(1 <= N <= 100)$ — количество ваших соперников. В следующих $N$ строках находятся по одной строке $C_i(1 <= |C_i| <= 100)$ — программы ваших соперников. $C_i$ состоит из букв 'R', 'P', 'S'.

Формат выходного файла

Если не существует победной программы для вашего робота, выведите "IMPOSSIBLE". Иначе, выведите победную программу для своего робота. Длина вашей программы не должна превосходить $10^4$. Гарантируется, что если ответ существует, то существует ответ длиной не более $10^4$. Если существует несколько ответов, выведите любой из них.

Примеры:

Вход

3
R
S
P

Ответ

IMPOSSIBLE

Вход

1
RP

Ответ

Вход

2
RP
S

Ответ

RPP

( Temirlan Satylkhanov )
комментарий/решение(2) олимпиада

Задача №12.

Задача G. Камень… Ножницы… Бумага...

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Формат входного файла

Формат выходного файла

Примеры:

Вход

3
R
S
P

Ответ

IMPOSSIBLE

Вход

1
RP

Ответ

Вход

2
RP
S

Ответ

RPP

( Temirlan Satylkhanov )
комментарий/решение(2) олимпиада

Задача №13.

Задача F. UCL Fantasy

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Недавно Данияр начал увлекаться футболом. И сразу начал играть UCL Fantasy. Правила простые, каждый игрок собирает себе команду из 15 игроков(2 вратаря, 5 защитников, 5 полузащитников, 3 нападающих) играющих в Лиге чемпионов УЕФА. Каждый игрок за тур получает какие-то баллы в зависимости как он сыграл. Баллы можно получить за гол, за голевой пас, вратарю за сухую игру, отрицательный балл за удаления и т.д. Перед каждым туром Данияр выбирает состав на тур, состоящий из 11 игроков и среди них выбирает капитана. В составе всегда должен быть ровно один вратарь, и возможны следующие схемы: 5(защитника)-4(полузащитника)-1(нападающий), 5-3-2,5-2-3,4-5-1,4-4-2,4-3-3,3-5-2,3-4-3. Тогда очки Данияра, это будет сумма баллов его состава(11 игроков) + баллы его капитана(т.е баллы капитана удваиваются). Данияр знает баллы всех своих игроков, помогите ему выбрать состав на тур, чтобы максимизировать количество его очков.

Формат входного файла

В 15 строках находятся информация о игроках: $name_i(1 <= |name_i| <= 20)$,$position_i$ и $p_i(-10 <= p_i <= 100)$ — имя или фамилия игрока, позиция в которой он играет и его баллы за тур. Гарантируется, что 2 вратаря, 5 защитников, 5 полузащитников, 3 нападающих. $position_i$ может быть одной из : GK — вратарь, DF — защитник, MF — полузащитник, FW — нападающий.

Формат выходного файла

Выведите, максимальное количество очков, которые может получить Данияр.

Пример:

Вход

Messi FW 10
Pique DF 6
Tadic FW 2
Coutinho MF 3
Stegen GK 7
Salah MF 2
Ziyech MF 6
Onana GK 6
Beek MF 8
Son MF 0
Alba DF 8
Suarez FW 8
Blind DF 6
Ligt DF 6
Roberto DF 6

Ответ

Замечание

Messi будет капитаном и состав будет таким:

( Temirlan Satylkhanov )
комментарий/решение(3) олимпиада

Задача №14.

Задача F. UCL Fantasy

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Формат входного файла

Формат выходного файла

Выведите, максимальное количество очков, которые может получить Данияр.

Пример:

Вход

Messi FW 10
Pique DF 6
Tadic FW 2
Coutinho MF 3
Stegen GK 7
Salah MF 2
Ziyech MF 6
Onana GK 6
Beek MF 8
Son MF 0
Alba DF 8
Suarez FW 8
Blind DF 6
Ligt DF 6
Roberto DF 6

Ответ

Замечание

Messi будет капитаном и состав будет таким:

( Temirlan Satylkhanov )
комментарий/решение(3) олимпиада

Задача №15.

Задача F. K-sort

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

У Есмахана есть массив $A$ состоящий из $N$ целых чисел $A_0,A_1,..,A_{N-1}$. Массив называется $k$-сортируемым, если массив можно отсортировать по неубыванию c помощью нескольких(возможно ноль) таких операции: выбрать индекс $i(0 <= i < N)$ и поменять местами $i$-й и $((i + k)$ mod $N$)-й элементы массива. Операция $a$ mod $b$ означает остаток $a$ при делении на $b$. Например, $7$ mod $3$ = 1, $8$ mod $4$ = 0, $5$ mod $11$ = 5. Массив считается отсортированным по неубыванию, если каждый элемент(кроме первого) не меньше чем предыдущий элемент. Есть $Q$ запросов, каждый запрос состоит из одного целого числа $k$. Для каждого запроса нужно определить, является ли массив $A$ $k$-сортируемым.

Формат входного файла

В первой строке находятся два целых числа $N,Q(1 <= N,Q <= 300000)$. Во второй строке находятся $N$ целых числа $A_0,A_1, ..., A_{N - 1}(1 <= A_i <= 10^9)$. В следующих $q$ строках находятся по одному целому числу $k_i(1 <= k_i <= N)$.

Формат выходного файла

В $q$ строках выведите по одному целому числу — в $i$-й строке выведите $1$, если массив $A$ является $k_i$-сортируемым, иначе выведите 0.

Система оценки

Это задача состоит из 5 подзадач и 25 тестов, каждый тест оценивается в 4 балла. В подзадачах выполняются следующие дополнительные ограничения:

$1 <= N,Q <= 100$. Тесты 1 -- 4
$1 <= N <= 100000, Q = 1$, $k_1 = N$. Тесты 5 -- 7
$1 <= N,Q <= 2000$. Тесты 8 -- 11
$1 <= N,Q <= 50000$. Тесты 12 -- 15
$1 <= N,Q <= 300000$. Тесты 16 -- 25

Пример:

Вход

Ответ

Замечание

Изначально $A={3,2,2,4}$, т.е $A_0 = 3, A_1 = 2, A_2 = 2, A_3 = 4$. Массив $3$-сортируемый, потому что с помощью следующих операции можно отсортировать:

Выберем $i = 1$, тогда $(i + 3)$ mod $N = (1 + 3)$ mod $4 = 0$. Т.е поменяем местами $A_1$ и $A_0$. Получиться $A = {2,3,2,4}$.
Выберем $i = 2$, тогда $(i + 3)$ mod $N = (2 + 3)$ mod $4 = 1$. Т.е поменяем местами $A_2$ и $A_1$. Получиться $A = {2,2,3,4}$.

( Temirlan Satylkhanov )
комментарий/решение(1) олимпиада

Задача №16.

Задача B. Тетрис

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

BThero играет в тетрис. Поле можно представить как прямоугольник с шириной $W$ и бесконечной высотой. Для удобства скажем что прямоугольник находится на двумерной системе координат. Левая нижняя клетка поля имеет координаты $(1, 1)$, а правая нижняя — $(W, 1)$. В игре последовательно произошли $q$ событий двух типов:

На поле падает новый прямоугольник покрывающий $x$-отрезок $[l,r]$ и высотой $h$. Он начинает падать с бесконечной высоты и падает до тех пор, пока не уткнется в другой прямоугольник или на дно поля. Заметьте, что в данной вариации тетриса двигать прямоугольники вы не можете.
Поступает запрос с одним целым числом $y$. Надо ответить, сколько клеток на высоте $y$ уже заняты прямоугольниками.

Помогите BThero эффективно обработать все события!

Формат входного файла

В первой строке даны два целых числа $W$ и $q$ ($1 <= W <= 10^6$, $2 <= q <= 10^5$). В последующих $q$ строках идут описания событий. Сперва дается одно целое число $t$ — тип события. Если $t = 1$, это событие первого типа и вам дополнительно даются три целых числа $l$, $r$ и $h$ ($1 <= l <= r <= W$, $1 <= h <= 10^6$). Если $t = 2$, это событие второго типа и вам дополнительно дается одно целое число $y$ ($1 <= y <= 10^9$). Гарантируется, что есть хотя бы одно событие первого типа и хотя бы одно событие второго типа.

Формат выходного файла

Выходной файл должен содержать ответы на все события второго типа.

Система оценки

Данная задача содержит $6$ подзадач, в которых выполняются следующие ограничения:

$q <= 5000$. Оценивается в $20$ баллов.
Гарантируется, что самое первое событие первого типа, а все последующие — второго типа. Оценивается в $10$ баллов.
Гарантируется, что все прямоугольники имеют высоту $1$, ширину $1$ и для всех событий второго типа $y <= 10^6$. Оценивается в $10$ баллов.
Гарантируется, что все прямоугольники имеют ширину $1$ и для всех событий второго типа $y <= 10^6$. Оценивается в $20$ баллов.
Для всех событий второго типа $y <= 10^6$. Оценивается в $20$ баллов.
Исходные условия задачи. Оценивается в $20$ баллов.

Пример:

Вход

Ответ

Замечание

( Temirlan Satylkhanov )
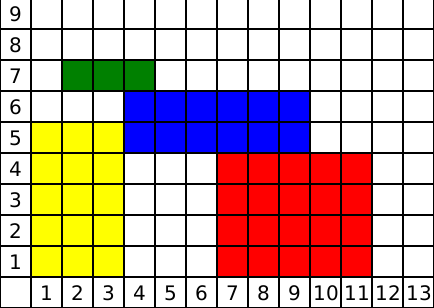
комментарий/решение олимпиада

Задача №17.

Задача C. Футболки

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Тима любит футболки. В городе есть очень крутой магазин футболок, который продает футболки $n$ цветов пронумерованных от $1$ до $n$, включительно. В течении $k$ дней магазин проводит масштабную акцию, где они будут продавать футболки некоторых цветов за полцены. Магазин опубликовал у себя на сайте таблицу $a$, где $a_{i,j}$ обозначает действует ли акция в $j$-й день на футболку цвета $i$ (1 если действует, иначе 0). У Тимы есть порядок предпочтений цветов $p$, который является перестановкой чисел от $1$ до $n$. Любимый цвет Тимы это цвет $p_1$, второй самый любимый это цвет $p_2$ и т.д. Каждый день в течении $k$ дней он будет приходить в магазин, и среди тех цветов на которые действует акция в тот день, он купит одну футболку с наиболее любимым цветом. Формально, в $i$-й день он выберет самый минимальный $j$, что $a_{i,{p_j}} = 1$ и купит одну футболку с цветом $p_j$. Если в тот день нет ни одного цвета, на который действует акция, то он ничего не покупает. Тима хранит $p$ в тайне. Какое максимальное количество различных цветов может оказаться среди футболок, которое он купил за $k$ дней?

Формат входного файла

В первой строке задано два целых числа $n$ и $k$ ($1 <= n <= 10^5$, $1 <= k <= 14$). В следующих $n$ строках записано по $k$ символов — элементы $a$. Каждый символ является либо «0», либо «1».

Формат выходного файла

Выведите одно целое число — максимальное количество различных цветов, которое может оказаться среди футболок.

Система оценки

Данная задача содержит $6$ подзадач, в которых выполняются следующие ограничения:

Тесты из условия. Оценивается в $0$ баллов.
$n$, $k <= 2$. Оценивается в $9$ баллов.
$n$, $k <= 8$. Оценивается в $18$ баллов.
$n$, $k <= 14$. Оценивается в $22$ баллов.
$n <= 10000$, $k <= 14$. Оценивается в $29$ баллов.
Исходные условия задачи. Оценивается в $22$ баллов.

Примеры:

Вход

Ответ

Вход

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №18.

Задача A. Спортивные программисты

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Ассоциация спортивных программистов Казахстана решила организовать забег перед Олимпиадой. В забеге приняло участие $N$ человек. На старте бегуны расположились друг за другом в линию в порядке от $1$ до $N$. Когда был дан свисток, участники забега ринулись с мест, при этом поддерживая порядок кто за кем бежит. Участник с номером $1$ бежит первым, а участник с номером $N$ — последним. Но какой же это забег, если никто никого не обгоняет? Обгон происходит, когда у одного из участников развязываются шнурки на кроссовках. Пока бегун завязывает свои шнурки, следующие за ним участники могут его обогнать. Рассмотрим на примере. При $N = 5$ изначальная линия бегунов выглядит так: $1$ $2$ $3$ $4$ $5$. В процессе у участника с номером $2$ развязываются шнурки. Пока он их завязывает, предположим, что двоим участникам удается его обогнать. Тогда порядок участников становится: $1$ $3$ $4$ $2$ $5$. Если теперь у бегуна с номером $4$ возникнут проблемы со шнурками, из-за чего он пропустит, например, одного человека вперед, то линия станет: $1$ $3$ $2$ $4$ $5$. Вам дается $N$ и порядок в котором бегуны финишировали. Вам необходимо узнать минимальное количество участников, у которых могли развязаться шнурки во время забега.

Формат входного файла

В первой строке находится одно целое число $N(1 <= N <= 200000)$. Во второй строке находятся $N$ целых чисел $p_1, p_2, \ldots, p_N$($1 <= p_i <= N$, $p_i \neq p_j$ если $i \neq j$) — первым финишировал бегун $p_1$, вторым был $p_2$, \dots, последним — $p_N$.

Формат выходного файла

Выведите одно целое число — ответ на задачу.

Примеры:

Вход

6
1 2 5 4 3 6

Ответ

Вход

3
1 2 3

Ответ

Замечание

Разберем первый пример. Изначальная линия: $1$ $2$ $3$ $4$ $5$ $6$. Один из возможных вариантов событий: Сначала развязался шнурок у бегуна с номером $4$ и его обогнал $5$-й. Линия стала равной $1$ $2$ $3$ $5$ $4$ $6$. После этого развязался шнурок у бегуна с номером $3$ и его обогнали бегуны $5$ и $4$. Линия стала равной $1$ $2$ $5$ $4$ $3$ $6$. Можно показать, что если бы шнурки развязались у менее чем двух бегунов, тогда невозможно было бы получить нужный порядок. ( Temirlan Satylkhanov )
комментарий/решение(7) олимпиада

Задача №19.

Задача A. Работать или отдыхать?

Ограничение по времени:

1.5 секунд

Ограничение по памяти:

256 мегабайт

У Ади есть $S$ тенге. В каждый из следующих $N$ дней он решил, что будет либо целый день работать, либо целый день отдыхать. Он высчитал, что если будет работать в $i$-й день, то заработает $a_i$ тенге. А чтобы отдохнуть в $i$-й день, он потратит $b_i$ тенге. Другими словами, если в $i$-й день он будет работать, то количество его денег увеличиться на $a_i$, а если будет отдыхать, то количество денег уменьшится на $b_i$. Какое максимальное количество дней он может отдохнуть? При этом, ни в какой момент времени количество его денег не должно быть отрицательным.

Формат входного файла

В первой строке находятся два целых числа $N$ и $S$($1 <= N <= 200000$, $0 <= S <= 10^9$) — количество дней и изначальное количество денег. В следующих $N$ строках находятся по два целых числа $a_i$ и $b_i(0 <= a_i,b_i <= 10^9)$.

Формат выходного файла

Выведите одно целое число — максимальное количество дней, в которые Ади может отдохнуть.

Примеры:

Вход

Ответ

Вход

Ответ

Замечание

В первом примере: в первый день он будет работать, а второй и третий день отдыхать. Во втором примере: он будет отдыхать в дни $2$, $4$ и $5$. ( Temirlan Satylkhanov )
комментарий/решение(2) олимпиада

Задача №20.

Задача C. Выборы в Массивтобе

Ограничение по времени:

2 секунды

Ограничение по памяти:

1024 мегабайта

В городе Массивтобе проводятся очередные выборы акима. Массивтобе -- современный город имеющий систему дорог в виде дерева. В нем есть $n$ домов соединенных $n - 1$ двусторонними дорогами так, что из каждого дома можно добраться до всех остальных передвигаясь по этим дорогам. Айбар — начинающий блогер, который хочет осветить выборы. Он решил снять видео социального опроса в котором он собирается идти по простому пути в городе и спрашивать за кого голосует жители каждого дома. Путь считается простым если он проходит по каждой вершине не более одного раза. Айбар знает, что видео не наберет много просмотров если в нем не будет доминантного кандидата. Кандидат считается доминантным если более половины опрошенных в видео голосуют за него. Всего есть $n$ кандидатов с номерами от $1$ до $n$. Вам дан список $v_1$, $v_2$, \dots, $v_n$, где значение $v_i$ означает, за кого голосуют жители $i$-го дома. Чтобы произвести как можно больше контента Айбар просит вас посчитать сколько есть различных путей в Массивтобе с доминантным кандидатом. Путь идущий из вершины $v$ в вершину $u$, считается таким же как и путь из $u$ в $v$.

Формат входного файла

В первой строке находится одно целое число $n$ ($1 <= n <= 77777$). Во второй строке находятся $n$ целых чисел $v_1$, $v_2$, \dots, $v_n$ ($1 <= v_i <= n$). В каждом из следующих $n - 1$ строк находятся два целых числа $a$ и $b$ ($1 <= a, b <= n$, $a \neq b$) означающие существование дороги между домами $a$ и $b$.

Формат выходного файла

Выведите одно целое число — количество различных путей с доминантным кандидатом.

Система оценки

Данная задача содержит $9$ подзадач, в которых выполняются следующие ограничения:

Примеры из условия. Оценивается в $0$ баллов.
$n <= 100$. Гарантируется, что $a_i=i$, $b_i=i+1$ для всех $i$ ($1 <= i < n$). Оценивается в $6$ баллов.
$n <= 2000$. Гарантируется, что $a_i=i$, $b_i=i+1$ для всех $i$ ($1 <= i < n$). Оценивается в $7$ баллов.
$n <= 2000$. Оценивается в $8$ баллов.
Гарантируется, что $a_i=1$, $b_i=i+1$ для всех $i$ ($1 <= i < n$). Оценивается в $10$ баллов.
$v_i <= 100$. Гарантируется, что $a_i=i$, $b_i=i+1$ для всех $i$ ($1 <= i < n$). Оценивается в $9$ баллов.
Гарантируется, что $a_i=i$, $b_i=i+1$ для всех $i$ ($1 <= i < n$). Оценивается в $13$ баллов.
$v_i <= 100$. Оценивается в $12$ баллов.
Исходные условия задачи. Оценивается в $35$ баллов.

Пример:

Вход

Ответ

( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №21.

Задача B. AB

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

$N$ школьников из классов А и Б выстроены в ряд. $i$-й школьник в ряду сказал число $c_i$ -- сколько школьников не с его класса стоят левее в ряду. Вам дан перемешанный массив $c$. Восстановите любое возможное изначальное расположение учеников.

Формат входного файла

В первой строке находится одно целое число $N(1 <= N <= 1.5\cdot 10^6)$. Во второй строке находятся $N$ целых числа $x_1,x_2,...,x_N(0 <= x_i <= N)$ — перемешанный массив $c$.

Формат выходного файла

Выведите изначальное расположение учеников в виде строки длины $N$ ---состоящей из символов $a$ и $b$. Гарантируется, что существует хотя бы одна такая строка. Если есть несколько ответов, выведите любое из них.

Система оценки

Данная задача содержит $9$ подзадач, в которых выполняются следующие ограничения:

Примеры из условия. Оценивается в $0$ баллов.
$N <= 10^5$. Гарантируется, что существует ответ при которым нет не одного ученика с B класса. Оценивается в $6$ баллов.
$N <= 20$. Оценивается в $10$ баллов.
$N <= 10^5$. Гарантируется, что существует ответ при которым есть не более 2 ученика с B класса. Оценивается в $8$ баллов.
$N <= 10^5$. Гарантируется, что существует строка, что полученный массив для этой строки $c$ будет равен массиву $x$ без перемешивание. Оценивается в $14$ баллов.
$N <= 40$. Оценивается в $13$ баллов.
$N <= 2000$. Оценивается в $10$ баллов.
$N <= 300000$. Оценивается в $27$ баллов.
$N <= 1500000$. Оценивается в $12$ баллов.

Примеры:

Вход

4
1 0 2 0

Ответ

bbab

Вход

5
0 0 2 1 3

Ответ

bbaba

Замечание

Если $bbab$ изначальное расположение школьников, то тогда $c_1 = 0, c_2 = 0, c_3 = 2, c_4 = 1$. Перемешав можно получить массив [1,0,2,0]. ( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №22.

Задача D. Витя - черепашка ниндзя 2

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Дается прямоугольная таблица $N \times M$, в каждой клетке записано какое-то число. Витя находится в левой верхней клетке, его цель добраться до правого нижнего угла. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). За посещение клетки, Витя должен платить число указанное в этой клетке. Дончик владелец таблицы. Он решил сделать скидку своему другу Вите, разрешив платить только за самые дорогие(наибольшие по значению) $K$ клеток на его пути от левого верхнего угла в правый нижний. Какое минимальное количество денег потратит Витя для достижения своей цели?

Формат входного файла

В первой строке даны три целых числа $N,M$ и $K$ ($1 <= N, M <= 500$, $1 <= K <= N + M - 1$). В следующих $N$ строках даны по $M$ целых чисел — $j$-е число на $i$-й строке $a_{i, j}$ ($0 <= a_{i, j} <= 500$) является числом на клетке в $i$-й строке и $j$-м столбце таблицы.

Формат выходного файла

Выведите одно целое число — ответ на задачу.

Примеры:

Вход

Ответ

Вход

Ответ

Замечание

Зеленым выделен путь Вити.

В первом примере, он заплатит за все посещенные клетки. Во втором примере, оптимально будет пройти через клетки со значениями $1,3,4,4,0,1,0$, и заплатит за максимальные два($K = 2$) из них, т.е $4 + 4 = 8$. ( Temirlan Satylkhanov )
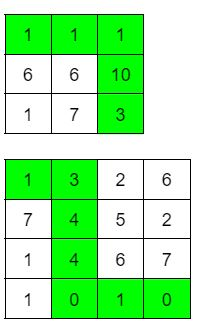
комментарий/решение(1) олимпиада

Задача №23.

Задача A. Три города

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

В одной маленькой стране есть всего три города и три платных двухсторонних дорог. Первая дорога проходит между городами $1$ и $2$, проехать по этой дороге стоит $A$ тенге. Вторая дорога проходит между городами $2$ и $3$, проехать по этой дороге стоит $B$ тенге. Третья дорога соединяет города $1$ и $3$, проехать по этой дороге стоит $C$ тенге. Парасату нужно доехать из города $1$ в город $3$ потратив как можно меньше денег.

Формат входного файла

В единственной строке находятся три целых числа $A$, $B$, $C$($1 <= A,B,C <= 5000$).

Формат выходного файла

Выведите минимальную стоимость добраться из города $1$ в город $3$.

Система оценки

Данная задача состоит из $10$ тестов. Каждый тест оценивается в $10$ баллов.

Примеры:

Вход

10 7 15

Ответ

Вход

200 300 700

Ответ

Замечание

Во втором примере: Парасату выгодно поехать через город $2$. ( Temirlan Satylkhanov )
комментарий/решение(4) олимпиада

Задача №24.

Задача C. Без переноса

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Маленький Дамир еще не научился делать переносы при сложении чисел. Но он отлично справляется со сложением чисел, где не нужно делать перенос. Например, Дамир не сможет посчитать $27+5$, но легко посчитает $31421 + 6374 + 3$. У вас есть $N$ чисел. Вам нужно среди них выбрать максимальное количество чисел, которых можно сложить без переноса.

Формат входного файла

В первой строке находится одно целое число $N(1 <= N <= 18)$. Во второй строке находятся $N$ целых числа $a_1, a_2, ..., a_N$($1 <= a_i <= 10^8$).

Формат выходного файла

Выведите ответ на задачу.

Система оценки

Данная задача состоит из $10$ тестов. Каждый тест оценивается в $10$ баллов.

Тест 1. Пример из условия.
Тесты 2-4: $n = 2$.
Тесты 5-7: $1 <= a_i <= 9$.
Тесты 8-10: без дополнительных ограничении.

Пример:

Вход

5
8 45 32 27 111

Ответ

Замечание

В первом примере можно выбрать три числа: $45$,$32$,$111$. ( Temirlan Satylkhanov )
комментарий/решение(1) олимпиада

Задача №25.

Задача B. Цена за мороженное

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Вы продаете мороженное. Себестоимость одного мороженного $k$ тенге. Это значит, что если вы продаете одно мороженное по $x$ тенге, тогда прибыль с одного мороженного будет $x - k$ тенге. Есть $n$ клиентов, для каждого клиента $i$ известно максимальная сумма денег $s_i$ тенге, которую он готов потратить на мороженное. Каждый клиент купить столько мороженного, сколько сможет купить. Выберите цену мороженного таким образом, чтобы максимизировать суммарную прибыль.

Формат входного файла

В первой строке находятся два целых числа $n,k$($1 <= n <= 2 \cdot 10^5$, $0 <= k <= 10^6$) — количество клиентов и себестоимость одного мороженного. Во второй строке находятся $n$ целых числа $s_1, s_2, \cdots, s_n$($1 <= s_i <= 10^6$).

Формат выходного файла

Выведите максимальную возможную прибыль.

Примеры:

Вход

5 2
8 9 10 15 12

Ответ

Вход

3 20
15 10 20

Ответ

Замечание

В первом примере одно мороженное выгодно продавать по $7$ тенге. Тогда четвертый клиент купить 2 мороженное, а остальные 4 по одному. Всего продадим 6 мороженных. Прибыль с одного мороженного $5$($7 - 2$) тенге, тогда суммарная прибыль $6 \cdot 5 = 30$ тенге. ( Temirlan Satylkhanov )
комментарий/решение олимпиада

Задача №26.

Задача E. Покраска графа

Ограничение по времени:

1 секунда

Ограничение по памяти:

256 мегабайт

Дан ориентированный ацикличный граф из $N$ вершин и $M$ ребер. Вершины пронумерованы целыми числами от $1$ до $N$. Причем в графе нет ребра из вершины $1$ в вершину $N$. Все вершины изначального белого цвета. Мансуру нужно покрасить ровно $B$ вершин в черный цвет. После покраски удаляются все ребра у которых оба конца одного цвета. Помогите Мансуру покрасить $B$ вершин таким образом, чтобы нельзя было добраться из $1$ в $N$ после удаления всех ребер у которых оба конца одного цвета.

Формат входного файла

Каждый тест содержит несколько наборов входных данных. Первая строка содержит одно целое число $T$($1 <= T <= 100$) — количество входных данных. Первая строка каждого набора входных данных содержит три целых числа $N$,$M$ и $B$($3 <= N <= 10^5$, $0 <= M <= min(2 \cdot 10^5,\frac{N \cdot (N - 1)}{2})$, $1 <= B <= N$). Следующие $M$ строк каждого набора входных данных содержат по два целых числа $u$ и $v$($1 <= u, v <= N$, $u \ne v$, $(u,v) \ne (1, N)$) — задающие ориентированное ребро из вершины $u$ в вершину $v$. Гарантируется, что в графе нет цикл и повторяющихся ребер. Cумма $N$ по всем наборам входных данных не превосходит $10^6$. Cумма $M$ по всем наборам входных данных не превосходит $10^6$.

Формат выходного файла

Если невозможно покрасить нужным образом, выведите <<-1>>. Иначе, выведите $B$ различных целых числа — номера вершин которые нужно покрасить в черный цвет. Если есть несколько возможных ответов, выведите любую из них.

Пример:

Вход

Ответ

1 8 10 7 9
2 3

Замечание

( Temirlan Satylkhanov )
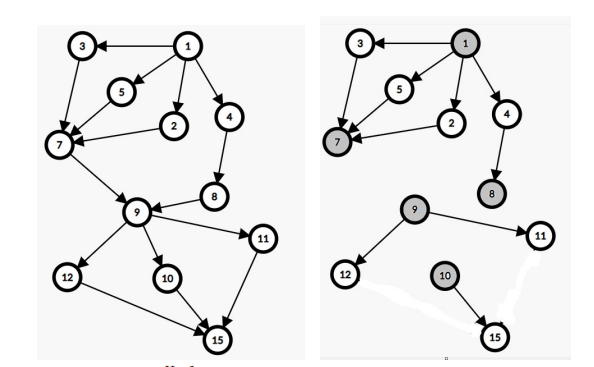
комментарий/решение олимпиада

Задача №27.

Задача F. XOR-сумма

Ограничение по времени:

2 секунды

Ограничение по памяти:

512 мегабайт

Дан массив $a$ из $n$ целых положительных чисел. Для каждого целого числа $k$ от $1$ до $m$ найдите значение $(a_1 \bmod k) \oplus (a_2 \bmod k) \oplus \ldots \oplus (a_n \bmod k)$. Здесь $\oplus$ обозначает операцию побитового XOR или исключающего ИЛИ. Данная операция существует во всех современных языках программирования, например, в языках C++,Python и Java она обозначена как <<^>>, в Pascal — как <>. Здесь $\bmod$ обозначает остаток от деления. То есть, $(a \bmod b)$ — остаток от деления числа $a$ на число $b$.

Формат входного файла

В первой строке задаются два целых числа $n$ и $m$ ($1 <= n, m <= 500\,000$). Во второй строке задаются массив $a_1, a_2, \ldots, a_n$ ($1 <= a_i <= m$).

Формат выходного файла

Выведите $m$ целых чисел через пробел, где $k$-е число равно значению $(a_1 \bmod k) \oplus (a_2 \bmod k) \oplus \ldots \oplus (a_n \bmod k)$.

Примеры:

Вход

4 5
2 5 4 2

Ответ

0 1 3 1 4

Вход

10 12
1 2 4 8 9 10 11 12 3 5

Ответ

0 1 1 1 0 1 0 5 9 3 11 1

( Temirlan Satylkhanov )
комментарий/решение олимпиада